1. Blog home
2. Present Value

Present Value

Present Value Intro

If someone offered you an envelope with $100 cash today or the same envelope with the same $100 one year from now would you take it now or wait a year and take it then?

You would take the money now, right? Intuitively you know this is right for two reasons:

1. There's always the risk that the money isn't going to be there for you in a year. Anything could happen, the person might lose it, they might change their mind or maybe they'll use some of it themselves forgetting it was meant for you.
2. You can take the envelope now, open it, take the $100 cash to your bank, deposit it and have your $100 plus any interest you would make over the year.

If these two points make sense, then you understand the time value of money.

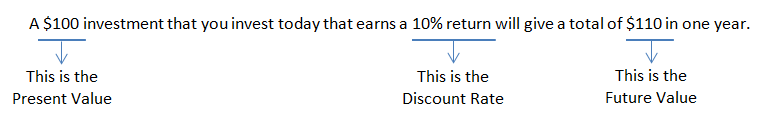
The Present Value is the current value of a future sum of money based on a specified rate of return.

The Discount Rate is the rate of return or interest rate that the investment will earn over a given period.

The Future Value is equal to a present sum of money plus the money earned over time at a specified rate of return.

Going from Present Value to Future Value

If you invest $100 today at 10% rate of return, you will end up with $110 in one year from now.

The $110 is made up of your initial investment of $100 and the 10% rate of return on top of that of $10.

This is what the formula looks like:

= $100 + ($100 * 10%) = $110

We can simplify this formula:

= $100 * (1+10%) = $110

What if you kept that investment going for two years instead of just one year, how much would that be worth?

If you invest $100 with a 10% rate of return for two years, you can use the same formula and multiply by (1+10%) for every additional year your money is invested.

So for a two year investment, you could use this formula:

= $100 * (1+10%) * (1+10%) = $121

Again you can simplify this formula:

= $100 * (1+10%)2 = $121

What if you keep that investment going for fourteen year instead, how much would that be worth?

= $100 * (1+10%)14 = $380

So here is the formula to go from Present Value (PV) to Future Value (FV) given a rate of return (r) and the number of periods (n):

PV * (1+r)n = FV

Going the other way: Future Value to Present Value

So now you know how to go from Present Value to Future Value, going the other way is the exact opposite.

What is the Present Value of a $110 sum of cash in one year given a discount rate of 10%?

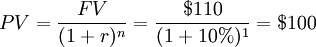
What is the Present Value of a $380 sum of cash in fourteen years from now given a discount rate of 10%?

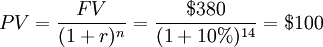
Making the Financial Decision

Calculating the future value of an investment given a rate of return and being able to discount future cash flows back to their present values is really helpful when comparing options and making decisions.

If your goal was to make as much money as you could this year and someone offered you $100 now or $120 in one year from now knowing whatever you invest now would earn you a 12% return, what would you do?

Option 1: take the $100 now and invest at 12% for one year.

FV in one year from now

= $100 * (1+12%) 1 = $112

Option 2: take the $120 one year from now

FV in one year from now = $120

Take the $120 in one year from now, you'll end up with more money that way.

Risk

Say you have two projects and you determine that both will pay you $120 one year from now but one is more risky than the other, which one would you choose?

If both have the same future value of $120 one year from now, you would pick the less risky project right? Why take additional risk without additional payoff but how does one quantify this risk?

There's a place in the Present Value formula where you can factor the element of risk and quantify it.

Project 1 is less risky. After looking at similar projects you estimate a discount rate of 10%.

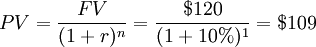
Project 2 is more risky. You estimate a discount rate of 10% plus an additional 4% for added risk for a total discount rate of 14%.

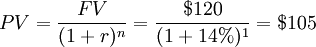
Based on two different discount rates which reflect the different risk level for each project, you see that the less risky project 1 is the better option since it has a higher present value.